背景误差协方差

• 11.3.1 删除时间均值
• 11.3.2 多元协方差：回归系数和不平衡变量
• 11.3.3 垂直协方差：特征向量/特征值和控制变量投影
• 11.3.4 水平协方差：递归滤波器长度标度（区域）或功率谱（全局）

预测（“首次估计”或“背景”）误差协方差是变分数据同化系统的重要输入。 它们影响分析与观察的契合度，也完全定义了远离观察的分析响应。 后者的影响在全球数据稀疏的地区尤其重要。 与集成滤波器数据同化技术（例如，集合调整卡尔曼滤波器，集合变换卡尔曼滤波器）不同，3/4D-Var 系统不会实时显式地生成预测误差协方差（尽管 4D-Var 和混合变分/集合 WRFDA 目前正在开发的数据同化技术隐含实现了与流相关的协方差。 相反，气候统计数据通常是离线估算的。 常用的方法是 “NMC-method”，其中使用预测偏差（例如 T+48 减去 T+24）统计量来近似预测误差协方差（Parrish 和 Derber，1992 年）。 ECMWF 的实验（Fisher，2003 年）表明，可以使用基于扰动观测/物理学的循环分析/预测集合预报系统获得更好的统计数据。

最近的进展允许通过例如网格转换（Desroziers，1997），各向异性递归滤波器（Wu 等，2002； Purser 等，2003）在 3D/4D-Var 中使用与流相关的预测误差协方差，或变分问题的观测空间公式（Daley 和 Barker，2001）。 通过使用预测模型在 4D-Var 的时间窗口内为不断变化的预测状态提供动态一致性，可以增强 4D-Var 中的流相关性（Rabier 等，1998）。 尽管如此，在 3/4D-Var 中指定和实现与流相关的误差协方差所需的实际工作仍然很重要。

统一的全球/区域 WRFDA 系统的开发及其在 WRF 社区中的广泛使用，需要开发高效，可移植的预测背景误差协方差计算代码。 许多应用程序还表明，如果人们花大力气计算特定于域的误差协方差，而不是使用 WRFDA 版本提供的默认统计信息，则可以获得更好的结果。 在本节中，描述了由 NCAR/MMM 开发的 gen_be_code，用于生成与 WRFDA 系统一起使用的预测错误统计信息。

背景误差协方差矩阵定义为

$$B = \overline{\epsilon \epsilon^T} \simeq \overline{x'x'^T} \tag{11.3}$$

其中，横线表示时间和/或地理区域的平均值。 真实的背景误差 $\epsilon$ 实际上未知，但被假定为在模型状态扰动 $x'$ 上可以很好地表示。

在标准 NMC 方法（Parrish and Derber，1992）中，扰动 $x'$ 由同时验证的两个预测（例如 24 小时减去 12 小时）之间的差给出。 然后可以通过对一段时间（例如一个月）内的这种预测差异求平均来获得背景误差的气候学估计。 （Fisher，2003）提出的另一种策略是利用集合预测输出，将 $x'$ 向量定义为集合扰动（集合减去集合均值）。 无论采用哪种方法，最终结果都是模型扰动矢量的集合，可以从中得出背景误差的估计值。 gen_be 实用程序旨在与预测偏差或基于集合的扰动一起使用。 使用 NMC 方法，$x'=x_{T2}-x_{T1}$，其中 $T2$ 和 $T1$ 是预测差异时间（例如，全球 48h 减去 24h，区域 24h 减去 12h）。 替代地，对于基于集合的方法，$x_k' = x_k - \bar{x}$，其中，上标是集合成员 $k=1，n_e$ 的平均值。 此阶段产生的二进制文件总数为 $n_f \times n_e$，其中 $n_f$ 是使用的预测次数（例如，对于 30 天，每 12 小时进行一次预测，$n_f = 60$）。 使用 NMC 方法，$n_e=1$（每时间 1 个预测差异）。 对于基于集合的统计，$n_e$ 是集合成员的数量。

如上所述，不是在模型空间 $x'$ 中而是在控制变量空间 $v$ 中指定 WRFDA 背景误差协方差，该变量通过（11.2）中定义的控制变量变换与模型变量（例如风分量，温度，湿度和表面压力）相关。

WRFDA 中同时要求（11.2）及其依赖。 为此，（离线）背景误差工具用于计算在 $U$ 变换中的预测误差协方差矩阵的分量。

以下小节将介绍此过程。

背景误差协方差生成代码 $gen_be$ 被设计为处理来自各种区域/全局模型（例如 ARW，MM5，KMA 全局模型，NFS 等）的数据，并对其进行处理以提供误差协方差统计数据以供变异数据同化系统使用。

初始的，与模型相关的 “阶段 0” 如图 11.2 所示。

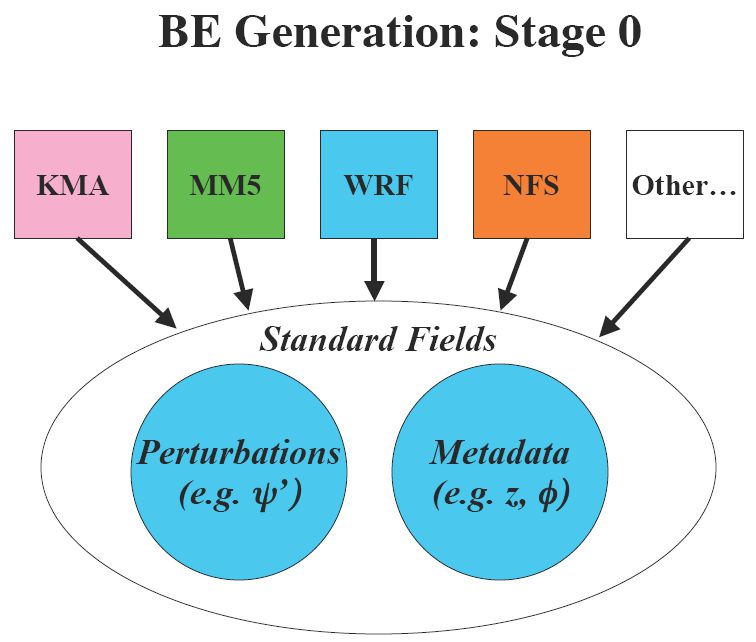
图 11.2：阶段 0 转换器在将特定于模型的数据（例如 ARW，KMA 全局模型等）转换为标准扰动字段和相关元数据（例如纬度，高度，陆地/海洋等）中的作用示意图。

11.3.1 删除时间均值

为了计算场之间的协方差，必须首先删除平均值。 这是在第一阶段实用程序 gen_be_stage1 中执行的。

11.3.2 多元协方差：回归系数和不平衡变量

gen_be 的第二阶段（gen_be_stage2）提供有关在 WRFDA 中用作控制变量的不平衡场 $\chi_u，T_u$ 和 $P_{su}$ 的统计信息。 不平衡控制变量定义为该场的完全和平衡（或相关）分量之间的差。 在背景误差计算的这一阶段，通过使用特定的预测变量场对场进行回归分析，对特定场的平衡分量进行建模（例如，流函数；有关更多详细信息，请参见 Wu 等人，2002 年）。 输出所得的回归系数，以供 WRFDA 的 $U_p$ 转换使用。 当前，执行了三个回归分析，得出了三组回归系数。

注意：为清楚起见，在本章的其余部分中已删除了扰动符号

• 速度势/流函数回归：$\chi_b(k)=c(k) \psi(k)$
• 温度/流函数回归：$T_b(k)=\sum_{k1}G(k1,k) \psi(k1)$
• 表面压力/流函数回归：$p_{sb}=\sum_{k1}W(k1)\psi(k1)$

垂直指标 k1 上的总和与质量场和风场之间的积分（静力）关系有关。 默认情况下，回归系数 $c，G$ 和 $W$ 不会水平变化，但是可以通过 bin_type namelist 变量放宽此假设，以便表示例如极地，中纬度和热带地区之间的动力和物理过程差异。 根据流函数来估计速度势偏差的标量系数 $c$ 随模型高度变化，以表示例如边界层物理的影响。 可以选择性地对所得系数进行纬度/高度平滑，以避免在纬度/高度的边缘出现虚假间断。

计算出回归系数后，不平衡分量计算方式为 $\chi_u(k) = \chi(k) - c(k)\psi(k)$, $T_u(k) = T(k) - \sum_{k1}G(k1,k)\psi(k1)$, and $p_{su}= p_s - \sum_{k1}W(k1)\psi(k1)$. 这些输出场，用于如下所述的空间协方差的后续计算。

11.3.3 垂直协方差：特征向量/特征值和控制变量投影

gen_be 的第三阶段（gen_be_stage3）计算控制变量变换的垂直分量所需的统计量。 这种计算涉及将模式各个高度的 3D 场投影到背景误差协方差的垂直分量的经验正交函数（EOF）上，Barker（2004）等人。 对于每个 3D 控制变量（$\psi$，$\chi_u$，$T_u$ 和 $r$），计算 B 的垂直分量，并进行特征向量分解。 保存所得的特征向量 E 和特征值 $\Lambda$ 以便在 WRFDA 中使用。

gen_be 代码可计算背景误差协方差矩阵的垂直分量的域平均值和局部值。 所得的 $K\times K$（K 为垂直级别数）气候垂直误差协方差矩阵 $B = E\Lambda E^T$ 的特征分解会同时产生域平均和局部特征向量 E 和特征值 $\Lambda$。 两组统计信息都包含在提供给 WRFDA 的数据集中，从而允许在运行时选择均质（域平均）或局部（非均质）背景误差方差与垂直相关性之间进行选择，Barker（2004）等人。 计算并存储了特征向量和特征值后，gen_be_stage3 的最后一部分就是将 3D 控制变量场的整个序列投影到 EOF 空间 $\mathbf{v_v} = U^{-1}_v \mathbf{v_p} = \Lambda^{-1/2} E^T \mathbf{v_p}$。 Having calculated and stored eigenvectors and eigenvalues, the final part of gen be stage3 is to project the entire sequence of 3D control variable fields into EOF space vv = U−1vvp = Λ−1/2ETvp.

11.3.4 水平协方差：递归滤波器长度标度（区域）或功率谱（全局）

WRFDA 所需的背景误差协方差数据的气候成分的最后一个方面是水平误差相关性，其表示形式是区域和全局模式下运行 WRFDA 之间的最大差异 - gen_be 的其余部分在区域和全局模式下基本相同。

在全局应用程序中（gen_be_stage4_global），将为 K 个垂直模型中的每个 3D 控制变量 $\psi$，$\chi_u$，$T_u$ 和相对湿度 $r$ 以及 2D 控制变量 $p_{su}$ 数据计算功率谱。 相比之下，在区域模式下，计算每个 2D 场的网格点之间的水平相关性，并将其作为距离的函数。 然后如 Barker 等（2004）所述，将高斯曲线拟合到数据中以提供用于递归滤波器算法的相关长度标度。